En esta unidad temática te familiarizarás con algunas de las siguientes transacciones:
- Amortización de préstamos
- Pagos de arrendamiento
- Planeación de las finanzas personales
- Calcular el valor de los ahorros en fechas futuras
- Calcular el monto que necesitas hoy para tener una cantidad específica en una fecha posterior
- Calcular el tiempo necesario para lograr una meta financiera
Para comprender cómo se realizan dichas transacciones y sobre todo para tomar las mejores decisiones al respecto, necesitas considerar el valor del dinero en el tiempo a través de la aplicación de algunas fórmulas matemáticas. Adicionalmente, también se requiere para la elaboración del presupuesto maestro con base en el cual se construyen los estados financieros proforma o proyectados, temas que abordaremos en esta unidad temática.
¿Qué es el valor del dinero en el tiempo?
El valor del dinero en el tiempo es uno de los aspectos más importantes de las finanzas; expliquémoslo de manera sencilla, si por ejemplo, en este momento tienes $100 (cien pesos) valen más el día de hoy que en el futuro y esto se debe básicamente a que el día de hoy los puedes invertir y ganar rendimientos. Sin embargo, esos mismos $100 (cien pesos) recibidos en el futuro no tedrán el mismo poder adquisitivo que tienen el día de hoy, dicho cambio en el valor del dinero tiene como principal causa el efecto inflacionario sobre los bienes y servicios que compramos. De tal manera que, “la relación que existe entre el tiempo, el interés y el poder de compra del dinero se conoce como valor del dinero en el tiempo” (Vidaurri, 2020, p.134).
A medida que vayas avanzando en los subtemas de este RDD irás comprendiendo mejor este interesante tema.
Del valor del dinero en el tiempo hay dos conceptos básicos que debemos comprender:
Valor futuro
Es el efectivo que se recibirá en una fecha futura. La técnica del valor futuro utiliza la capitalización para encontrar el valor futuro de cada flujo de efectivo.
Valor presente
Término que se usa para referirse al valor actual del dinero. La técnica del valor presente utiliza la tasa de descuento. Aunque el valor futuro es más atractivo por naturaleza, el valor presente es más útil para la toma de decisiones financieras (Gitman, 2012).
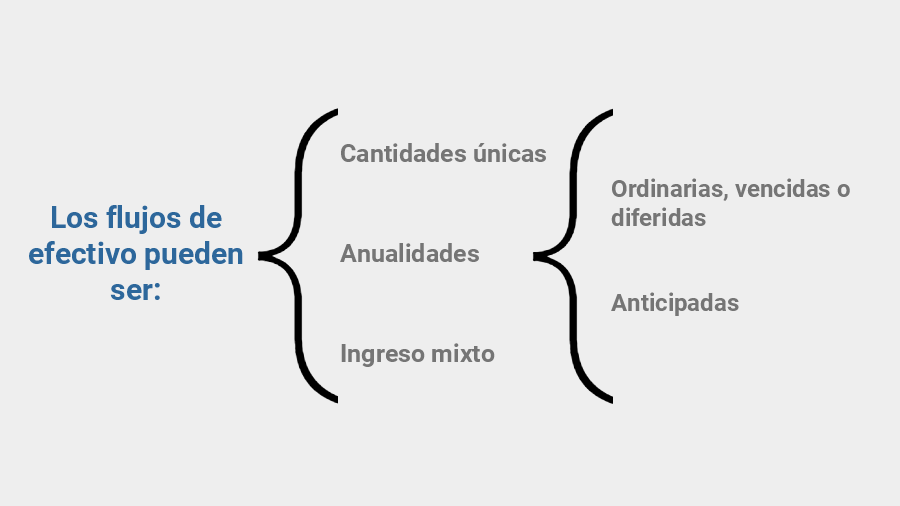
El valor del dinero se determina sobre los flujos de caja o flujos de efectivo. De acuerdo con Vidal y González (2014) el flujo de efectivo tiene como propósito determinar todas las entradas y salidas de dinero; es decir, los ingresos, costos, gastos e inversiones producidos por una empresa o proyecto en el futuro. Siguiendo a Gitman (2012) los flujos de efectivo (entradas y salidas de dinero) se pueden presentar como cantidades únicas (montos únicos), anualidades e ingreso mixto (figura 4.1).
Cantidad única
Cantidad global que se tiene actualmente (valor presente) o que se espera en una fecha futura (valor futuro); es cualquier cantidad que no se repite en forma periódica; por ejemplo: $100 pesos, $3,400 pesos o cualquier otra cantidad.
Anualidad
Son cantidades iguales que se repiten periódicamente durante un determinado
tiempo.
No necesariamente hace referencia a
pagos anuales, pueden ser quincenales,
mensuales, bimestrales etc. Las anualidades pueden ser de dos tipos: ordinarias,
vencidas o
diferidas y anticipadas.
4.2
Anualidades en este tema encontraras la explicación más detallada.
Ingreso mixto
Conjunto de flujos de efectivo periódicos y desiguales que no reflejan un patrón en particular. Por ejemplo, para el período uno $5,000 pesos, para el período dos $4,000 pesos, para el período tres $8,000 pesos, etc.
En los siguientes subtemas se abordarán el valor presente y valor futuro tanto de cantidades únicas, así como de anualidades.
El valor futuro de una cantidad única se puede determinar, al menos, de dos formas:
a. Línea de flujo de efectivo
b. Fórmula matemática
a. Línea de flujo de efectivo
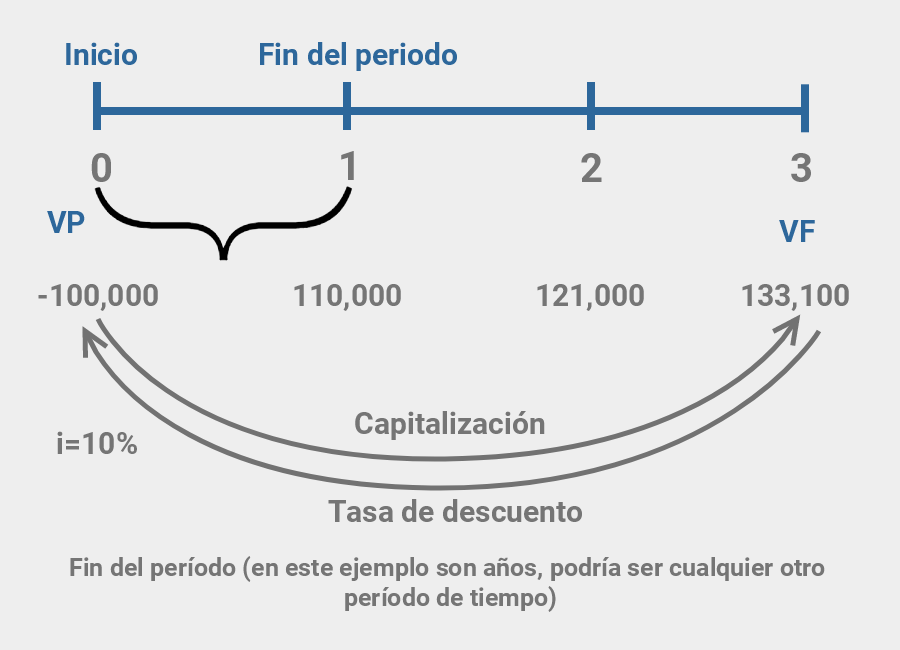
Ejemplo: En el supuesto que el día de hoy realizaras una inversión de $100,000 pesos con vencimiento a 3 años con una tasa de interés anual del 10% ¿Cuánto dinero recibirás al finalizar los tres años?
Hagamos los cálculos sobre la siguiente línea de flujo de efectivo.
A medida que vayas avanzando en los subtemas de este RDD irás comprendiendo mejor este interesante tema.
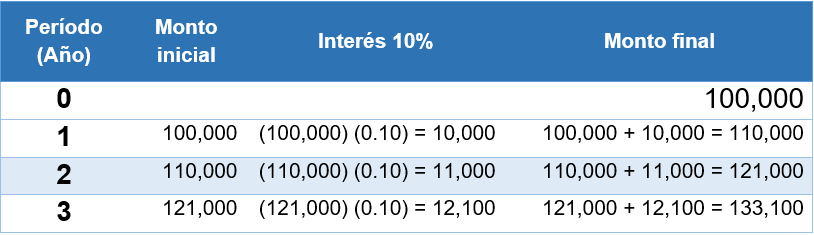
Las cantidades que aparecen en la línea de flujo de efectivo (figura 4.2), se calcularon tal como se indica en la tabla 4.1.
Como habrás notado usar la línea de flujo de efectivo resulta sencillo y muy práctico cuando se trata de pocos períodos de tiempo; sin embargo, puede ser laborioso cuando los cálculos son, por ejemplo, para más de 5 períodos. Para facilitar los cálculos contamos con la siguiente fórmula matemática:
b. Fómula matemática
La fórmula para calcular el valor futuro (VF) de una cantidad única es:
$$VF_n = {VP(1+i)^n}$$
Donde:
VP = Valor presente
VF = Valor futuro
i = Tasa de interés
n = Período de tiempo
Para el ejemplo que estamos trabajando quedaría:
$$VF_n = {VP(1+i)^n} = (100,000)(1.10)^3 = 133,100$$
Con los temas que has estudiado hasta este momento ya tienes los elementos suficientes para realizar la siguiente actividad de aprendizaje:
Actividad 4.1
Valor del dinero en el tiempo
DescargarEjemplo
Hasta el momento hemos calculado el valor futuro de una cantidad única, para encontrar el valor presente solo tienes que despejarlo de la fórmula.
Sigamos trabajando con el mismo ejemplo, solo que ahora vamos a enfocarnos en el valor presente, y la pregunta es: ¿cuánto tendrías que depositar hoy en una cuenta que paga el 10% de interés anual para recibir, al término de 3 años $133,100?
Contamos con la fórmula de valor futuro de cantidades únicas:
$$VF_n = {VP(1+i)^n}$$
Despejamos el valor presente:
$$VP = {VF\over(1+i)^n}$$
Ahora sustituimos los valores:
$$VP = {VF\over(1+i)^n} = {133,100\over(1+0.10)^3} = 100,000$$
Al proceso de encontrar los valores presentes también se le conoce como descuento de flujos de efectivo, dicho proceso es lo opuesto a la capitalización (ver figura 4.2). Y da respuesta a la pregunta: Sí puedo ganar un porcentaje i sobre mi dinero, por ejemplo el 10% ¿cuánto es lo máximo que estaría dispuesto(a) a invertir ahora por la oportunidad de recibir un valor futuro de dinero en 3 períodos de tiempo a partir de hoy? y la respuesta sería $100,000 pesos.
Anualidades
Una anualidad es una serie de flujos de efectivo iguales y periódicos durante un determinado tiempo (Besley, 2001; Gitman, 2012).
Las anualidades pueden ser de dos tipos:
a. Ordinarias, vencidas o diferidas
El flujo de efectivo (entrada o salida de efectivo) ocurre al final de cada período; estas anualidades son las más comunes en finanzas.
b. Anticipadas
El flujo de efectivo (entrada o salida de efectivo) ocurre al inicio de cada período.
Nota: en este curso nos centraremos en las anualidades ordinarias, vencidas o diferidas por ser las más utilizadas en el ámbito financiero.
Ejemplo
Para explicar el valor futuro de anualidades ordinarias empecemos con este ejemplo: al final de cada año inviertes $10,000 pesos durante los próximos 4 años a una tasa de interés del 10% anual. ¿Cuánto dinero obtendrás al finalizar el año 4?
Este problema se puede resolver de diferentes formas:
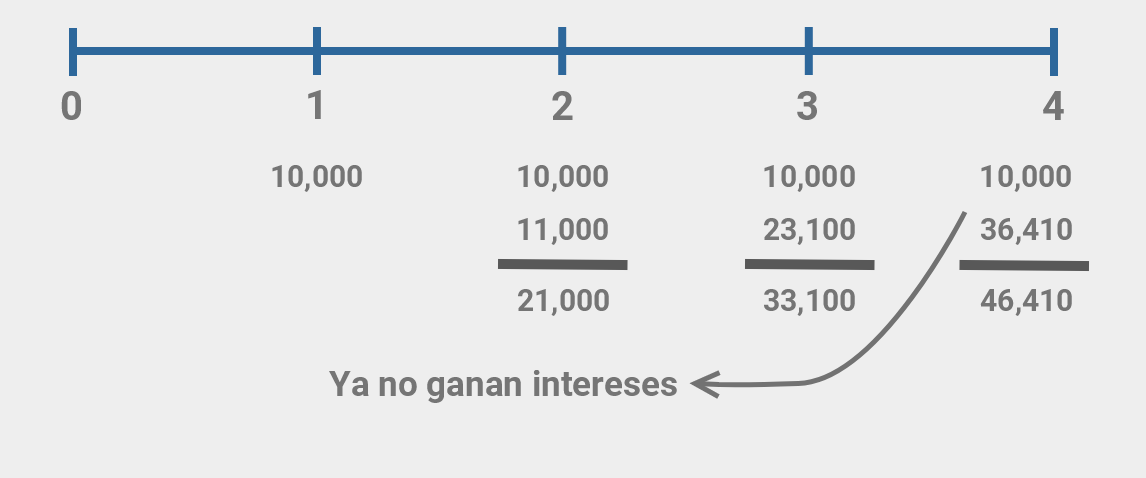
1. Utilizando la línea de flujo de efectivo
Expliquemos como se obtuvieron los cálculos en la linea de flujo de efectivo.
Invertimos $10,000 pesos al final del período 1, esos $10,000 pesos invertidos a una tasa del 10% anual ganan $1,100 pesos con lo que al final del período 2 se tendrían $11,000 pesos; al final del período 2 se invierten otros $10,000 pesos sumando un total de $21,000 pesos. Dicha cantidad se reinvierte y gana $2,100 pesos, entonces al final del período 3 se tienen $23,100 pesos que se suman a los $10,000 pesos que se están invirtiendo cada año dando un total de $33,100 pesos cantidad que se invierte y gana $3,310 dando un total de $36,410 pesos al final del período 4 y se le suman los $10,000 pesos (que ya no ganan intereses) en razon de que termina el plazo de la inversión, de tal manera que al final se tienen $46,410 pesos.
2. Calculando el valor futuro de los pagos individuales (cantidades únicas) y después sumarlos
Fórmula
$$VF_n = {VP(1+i)^n}$$
El VF del período 1 se capitaliza en 3 períodos.
$$VF_1 = {10,000(1+0.10)^3} = 13,310$$
El VF del período 2 se capitaliza en 2 períodos.
$$VF_2 = {10,000(1+0.10)^2} = 12,100$$
El VF del período 3 se capitaliza en 1 período.
$$VF_3 = {10,000(1+0.10)^1} = 11,000$$
El VF del período 4 no se capitaliza.
$$VF_4 = {10,000(1+0.10)^0} = 10,000$$
Total
$$46,410$$
3. Utilizando la fórmula de valor futuro de una anualidad ordinaria
$$VF_{An}= PA{(1+i)^n - 1\over i} = 10,000{(1+0.10)^4 - 1 \over 0.10} = 46,410$$
Donde:
VFAn = Valor futuro de una anualidad ordinaria a un período de tiempo
PA = Valor del pago igual o anualidad
i = Tasa de descuento
n = Período de tiempo
Ejemplo
Veamos un ejemplo en el que se podría utilizar la anualidad ordinaria.
Imagina que a la edad de 20 años empiezas a realizar depósitos anuales de $5,000 en una cuenta de ahorro que gana un 5% anual. Al final de 40 años, cuando tengas 60 años habrás ahorrado ($5,000) (40años) = 200,000; sin embargo, al retirar el dinero recibirás:
$$VF_{An}= PA{(1+i)^n - 1\over i} = 5,000{(1+0.5)^{40} - 1 \over 0.05} = $603,998.8712$$
Así, el valor del dinero en el tiempo habrá permitido que tus ahorros generen rendimientos compuestos durante 40 años.
Explicación
Utilizando los datos del ejemplo anterior (visto en valor futuro de anualidades ordinarias), ahora vamos a determinar el valor presente de una anualidad ordinaria.
Replanteamos el problema:
Al final de cada año inviertes $10,000 durante los próximos 4 años a una tasa de interés del 10% anual ¿Cuál es el valor presente de la anualidad ordinaria?
Para su cálculo cuentas con al menos dos opciones:
-
Utilizando la linea de flujo de efectivo y la fórmula de valor presentecomo si se tratara de cantidades únicas.
-
Fórmula de valor presente de una anualidad ordinaria.
Linea de flujo de efectivo y la fórmula de valor presente
Expliquemos cada una de dichas opciones
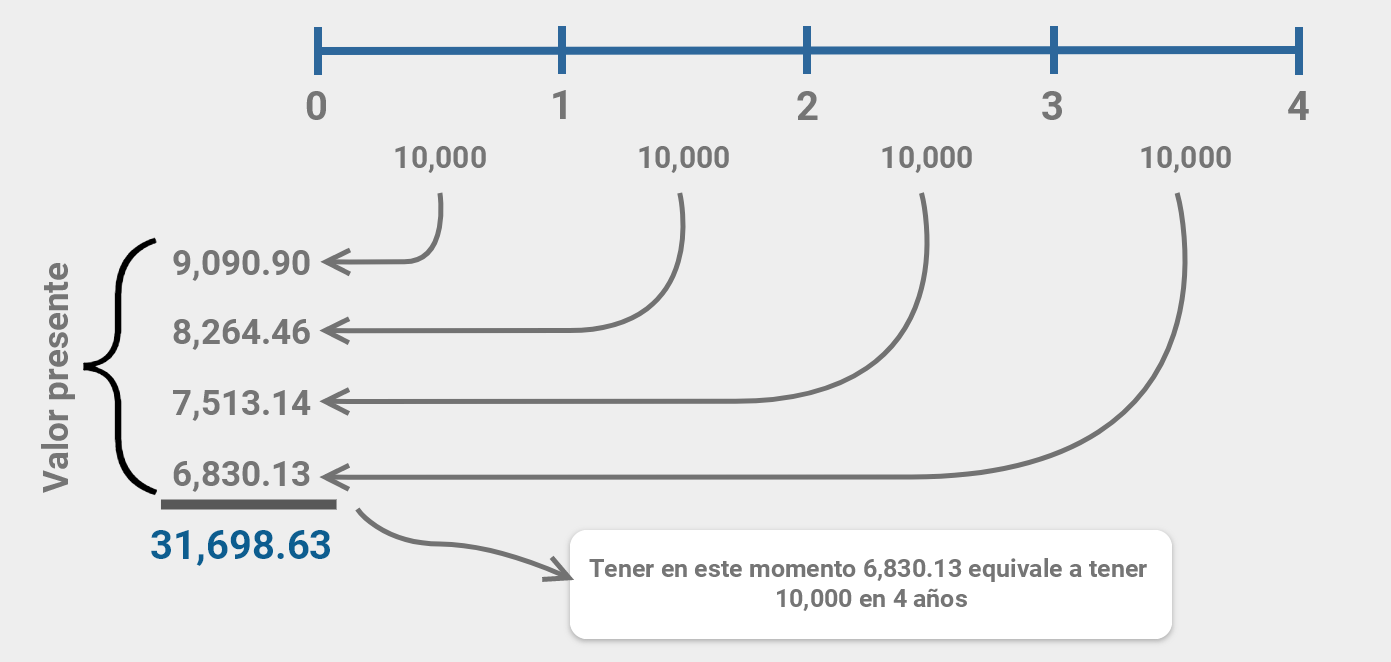
Cálculo del valor presente de anualidades ordinarias utilizando la linea de flujo de efectivo (figura 4.5) y la fórmula de valor presentecomo si se tratara de cantidades únicas.
A continuación se muestra la forma de calcular el valor presente de los flujos de efectivo.
$$VP = {10,000 \over 1.10^1} = 9,090.90$$
$$VP = {10,000 \over (1 + 0.10)^2} = 8,264.46$$
$$VP = {10,000 \over (1 + 0.10)^3} = 7,513.14$$
$$VP = {10,000 \over (1 + 0.10)^4} = 6,830.13$$
O bien, en lugar de calcular el valor presente para cada uno de los flujos de efectivo y luego sumarlos, podemos utilizar la siguiente fórmula:
$$VP_{An}= PA\left({{1- {1 \over (1+i)^n}} \over i}\right)$$
Donde:
P = Valor presente de una anualidad ordinaria a un período de tiempo
PA = Valor del pago igual o anualidad
i = Tasa de descuento
n = Período de tiempo
Para el ejemplo que estamos trabajando tenemos los siguientes datos:
$$PA = 10,000$$
$$i = 10%$$
$$n = 4$$
Sustituimos los valores en la fórmula:
$$VP_{An}= 10,000\left({{1- {1 \over (1+0.10)^4}} \over 0.10}\right)$$
$$VP_{An}= 31,698.63$$
El resultado: $31,698.63 corresponde al valor presente considerando todas las anualidades juntas.
Ejemplo
Al inicio de cada año invertimos $10,000 durante los próximos 4 años a una tasa de interés del 10% anual. ¿Cuánto dinero se obtiene al finalizar el período de inversión?
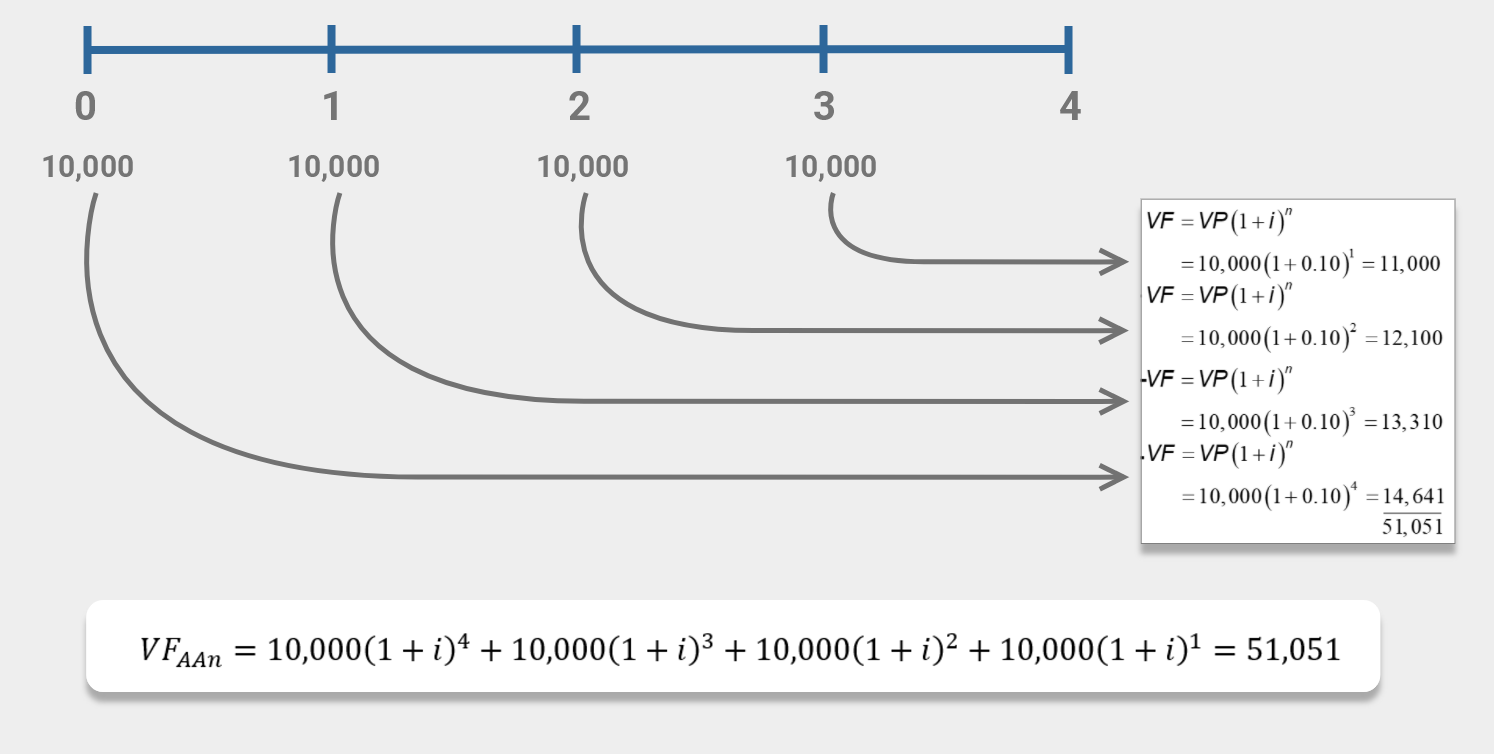
De igual manera que en los ejercicios anteriores, nos apoyaremos en la línea de flujo de efectivo (Figura 4.6), en la que se puede apreciar que nuestra primera inversión de $10,000 pesos (la que se realiza en el año 0) ganará intereses durante los años 1, 2, 3 y 4; la inversión que se realiza en el año 1 ganará intereses durante los años 2,3 y 4; y así sucesivamente; finalmente, la inversión que se hace en el año 3 gana intereses durante un año.
Para simplificar el cálculo del valor futuro de las 4 anualidades de $10,000 (cada una realizada al inicio del año), considerando que ganan el 10% anual, utilizaremos la siguiente fórmula:
$$VF_{Anualidad~Anticipada} = VP\left\lbrace\left[ {(1+i)^n - 1 \over i} * (1 + i) \right]\right\rbrace$$
Donde:
VF = Valor futuro
VP = Valor presente
i = Tasa de interés periódica
n = Número de períodos en los que se realiza la anualidad
Sustituyendo los datos en la fórmula nos queda:
$$VF_{AAn} = 10,000 \left\lbrace\left[ {(1.10)^4 - 1 \over 0.10} * (1.10) \right]\right\rbrace = 51,051$$
Si se conoce el valor futuro de una anualidad anticipada y se desconoce el valor presente, éste se puede calcular, lo único que tendrás que hacer es despejar la variable de la fórmula anterior.
Finalmente, es importante hacer énfasis en las siguientes consideraciones:
-
La diferencia entre una anualidad ordinaria y una anticipada es que, en ésta última cada uno de los pagos genera intereses durante un año adicional.
-
Las anualidades anticipadas regularmente se aplican a los planes de ahorro en anualidades y a los contratos de rentas y arrendamiento en los cuales el arrendatario hace el pago inicial de la renta al principio del período.
Explicación
Una de las aplicaciones más importantes del interés compuesto es la que se relaciona con los préstamos liquidables con base en anualidades (pagos iguales) a través del tiempo, como por ejemplo los préstamos para la compra de automóviles y los créditos bancarios e hipotecarios, entre otros.
Si un préstamo debe pagarse con base en montos periódicos iguales (quincenales, mensuales, trimestrales, anuales, etc.) se dice que es un préstamo amortizable; es decir, un préstamo reembolsable mediante pagos iguales en un determinado período de tiempo.
Para saber detalladamente cómo será reembolsado un préstamo se realiza un programa de amortización. Éste muestra en forma precisa cómo será pagado un préstamo, indicando el pago requerido en cada fecha y especificando qué cantidad de dicho pago se destina al pago de intereses y qué cantidad al pago de capital o principal. Al proceso de saldar o liquidar una deuda se le llama amortizar.
Ejemplo
Al iniciar sus operaciones, una empresa pide a una institución bancaria un préstamo de $1,000,000 de pesos a una tasa de interés del 24% , y le conceden un plazo de seis meses para cubrir el adeudo. El interés que se paga se capitaliza mensualmente sobre saldos insolutos.
En el caso de que esta empresa pagara cantidades iguales para cada uno de los períodos de pago determinar:
-
El valor de los pagos iguales (anualidad).
-
La tabla de amortización del préstamo.
Lo primero que se debe hacer es determinar el monto de la cantidad igual que se pagará cada período (en nuestro ejemplo es cada mes), para ello tenemos esta fórmula:
$$PA = P\left({i(1+i)^n \over (1+i)^n - 1}\right)$$
Donde:
P = Valor presente o principal (cantidad prestada)
PA = Valor del pago igual o anualidad
i = Tasa de interés
n = Período de tiempo
Para nuestro ejemplo contamos con los siguientes datos:
$$P = 1,000,000$$
$$i = {0.24 \over 12} = 0.02$$
$$n = 6$$
Sustituimos los datos en la fórmula:
$$PA = P\left({i(1+i)^n \over (1+i)^n - 1}\right)$$
$$PA = 1,000,000{0.02(1+0.02)^6 \over (1+0.02)^6 - 1}$$
$$PA = 212,158.39$$
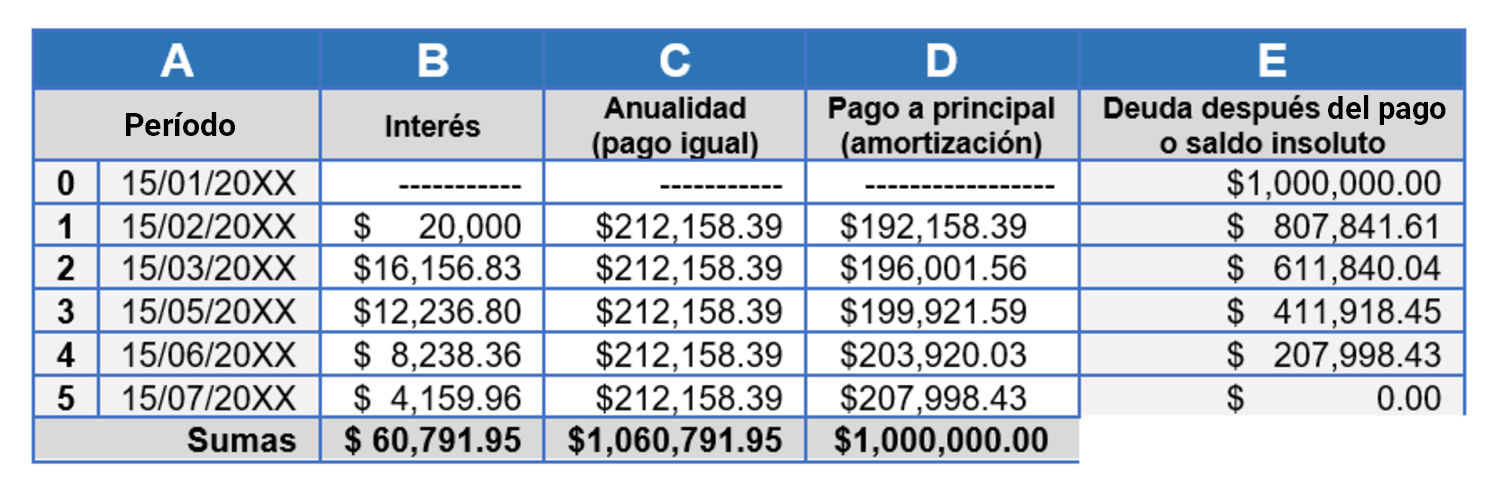
Ya calculamos el valor del pago igual o anualidad que se pagará cada período: $212,158.39. Ahora hay que determinar qué cantidad de ese pago es para pagar intereses y qué cantidad se destina para ir pagando (amortizando) el préstamo. Con los datos que tenemos ya podemos construir el programa de amortización del préstamo (tabla 4.2)
Explicación de la tabla de amortización:
Columna A
El período cero corresponde al presente, al momento en el que se adquiere la deuda. Los demás períodos corresponden a las fechas en las que se harán cada uno de los pagos hasta liquidar el préstamo.
Columna B
El interés del período se obtiene multiplicando el saldo insoluto del período anterior (que corresponde al saldo final de ese período y por tanto al inicial para el período que se trate) por la tasa de interés, en el ejemplo: para el período 1 el interés es igual a (1,000,000) (0.02) = 20,00; para el período 2 el interés es igual a (807,841.61) (0.02) = 16,156.83 y así sucesivamente.
Columna C
La anualidad, renta o cuota es el pago igual que se hará de manera periódica. Una parte de la anualidad es para pagar los intereses y lo que quede es para ir pagando a principal (la deuda).
Columna D
El pago a principal o a capital o amortización del préstamo es la cantidad que se está pagando a la deuda; en el ejemplo, de los 212,158.39 que se están pagando en cada período una parte son para cubrir intereses y la otra para ir pagando la deuda. Para calcular el pago a capital se restan los intereses a la anualidad, así en el período 1 se están abonando a la deuda $192,158.39 que resultó de la siguiente operación (212,158.39 – 20,000) = 192,158.39.
Columna E
La deuda después del pago o saldo insoluto corresponde a la deuda al final de cada período.
Es momento de movilizar tus aprendizajes sobre el tema realizando la siguiente actividad:
Actividad 4.2
Amortización de anualidades vencidas
Descargar¿Qué es la planeación financiera?
Para las empresas un elemento sumamente importante es la planeación financiera; ésta proporciona una guía que permite dirigir, coordinar y controlar las acciones que realiza la empresa orientadas al logro de sus objetivos. Vale la pena destacar que la planeación de efectivo (preparación del presupuesto de efectivo) y la planeación de utilidades (preparación de estados financieros proforma) son dos aspectos clave de la planeación financiera.
El proceso de la planeación financiera comienza con la elaboración de planes financieros a largo plazo o estratégicos y con base en estos se formulan los planes y presupuestos a corto plazo u operativos. No hay un consenso en cuanto al tiempo que se considera como corto o largo plazos; en este sentido, Gitman (2003) menciona que el corto plazo podría cubrir un período de uno a dos años y el largo plazo de más de dos años; también enfatiza que las empresas que están sujetas a altos grados de incertidumbre operativa, a ciclos de producción relativamente cortos, o a los dos, tienden a usar horizontes de planeación más cortos.
¿Qué es el presupuesto maestro?
El presupuesto maestro es un plan que integra los presupuestos financieros y operativos de una organización; muestra los recursos que requiere cada una de las áreas operativas para llevar a cabo sus actividades durante un período determinado.
La elaboración de los presupuestos financieros y operativos corresponde a los gerentes funcionales, aunque en algunas organizaciones existe un departamento o comité, dependiente del área de finanzas, que se encarga de realizar los presupuestos.
Por lo general el ciclo de elaboración de un presupuesto maestro inicia cuando la alta dirección, a través del departamento o comité de presupuestos, proporciona a los gerentes funcionales los pronósticos de venta y de utilidades que se espera durante del período y termina con la preparación de los estados financieros presupuestados (González, 2003).
En términos generales, el presupuesto maestro se integra por los siguientes presupuestos:
- Presupuesto de ingresos o de ventas
- Presupuesto de producción
- Presupuesto de requerimientos y compras de materia prima
- Presupuesto de mano de obra
- Presupuesto de gastos indirectos de fabricación
- Presupuesto de gastos de operación
- Presupuesto de inventarios iniciales y finales
- Presupuestos de costos de venta
- Presupuestos financieros, de efectivo, de capital y de requerimientos financieros
- Estados financieros presupuestados o proforma
Es importante mencionar que el estado de resultados presupuestado se basa en los presupuestos de operación y junto con los presupuestos financieros proporcionan información para la elaboración del estado de flujo de efectivo proforma y del estado de situación proforma.
Por último, la implementación y control del presupuesto maestro implican evaluar continuamente el desempeño real contra el presupuestado para detectar desviaciones y realizar los ajustes necesarios dirigidos al logro de los objetivos estratégicos de la organización.
El término proforma es sinónimo de proyectado, pronosticado, presupuestado y estimado; al hablar de estados financieros proforma nos estaremos refiriendo a estados financieros proyectados.
Estados financieros proforma
- Los proforma son estados que contienen, en todo o en parte, uno o varios supuestos o hipótesis con el fin de mostrar cuál sería la situación financiera o los resultados de las operaciones si éstos sucedieran.
- El objetivo de estos estados es proporcionar información anticipada sobre la situación financiera de la empresa si se trata del estado de situación financiera, o de las utilidades o pérdidas si se trata del estado de resultados.
- La base de los estados financieros proforma son los presupuestos.
Presupuesto
Estimación en términos monetarios tanto de los ingresos como de los egresos de un ente económico.
¿Quiénes utilizan los estados financieros proforma?
Accionistas y dueños
Para conocer la situación financiera
de la empresa
y
los
resultados esperados, con el fin de tomar decisiones.
Administradores
Para planear las operaciones, trazar
estrategias
facilitando
la
toma de decisiones que tienen impacto en el presente y en el futuro.
Acreedores y futuros acreedores
Para vigilar la seguridad de sus
créditos u
otorgar nuevos créditos.
Prospectos de accionistas
Para decidir sobre invertir o no en la
empresa
con
base en su situación financiera y resultados de operación.
Autoridades gubernamentales y crediticias
Estas instituciones se
auxilian de
los
estados financieros proforma como un
importante elemento que les
proporciona
información para evaluar la conveniencia de proporcionar
financiamiento
o no.
Al realizar la siguiente actividad de aprendizaje lograrás una mayor comprensión del tema: presupuesto maestro y estados financieros proforma.
Actividad 4.3
Presupuesto maestro y estados financieros proforma
DescargarTal y como lo estudiaste en esta unidad temática, el presupuesto maestro se conforma de un conjunto de presupuestos de operación y financieros a partir de los cuales se construyen los estados financieros proforma. Uno de esos presupuestos es el presupuesto de flujo de efectivo, con el que es posible calcular los flujos netos de efectivo (FNE) que son la base para evaluar proyectos de inversión, tema que verás en la siguiente unidad temática.